Momen Inersia – Dalam pelajaran fisika, kalian mempelajari tentang momen inersia. Apa yang dimaksud dengan momen inersia?Apa rumus monen inersia? Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian momen inersia, rumus dan contohnya secara lengkap.
Baca Juga : Hukum Newton
Pengertian Momen Inersia
Inersia adalah kecenderungan benda untuk mempertahankan keadaannya naik itu tetap diam atau bergerak. Benda yang sukar bergerak dikatakan memiliki inersia yang besar. Bumi yang selalu dalam keadaan rotasi memiliki inersia rotasi.
Pengertian momen inersia adalah ukuran besarnya kecendrungan berotasi yang ditentukan oleh keadaan benda atau partikel penyusunnya. Kecenderungan sebuah benda untuk mempertahankan keadaan diam atau bergerak lurus beraturan disebut dengan Inersia. Inersia disebut juga dengan Lembam. Keadaan alami benda ini berkaitan erat dengan hukum I Newton. Oleh karena itu, Hukum I Newton disebut juga hukum inersia atau hukum kelembaman.
Besarnya momen inersia suatu benda dipengaruhi oleh beberapa faktor, seperti massa benda, bentuk benda, letak sumbu putar dan jarak ke sumbu putar.
Rumus Momen Inersia
Perhatikan gambar dibawah ini!
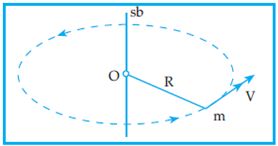
Sebuah partikel dengan massa m sedang berotasi pada sumbunya dengan jari-jari R. Momen inersia titik partikel tersebut dinyatakan sebagai hasil kali massa partikel dengan jarak partikel ke sumbu putar atau jari-jari. Dengan demikian, momen inersia sinyatakan dengan:
Baca Juga : Gerak Melingkar
I = m.R2
Keterangan:
I = Momen Inersia (Kg m2)
m = Massa partikel (Kg)
R = Jari-jari rotasi (m)
Momen inersia adalah hasil kali antara massa dengan kuadrat jarak massa terhadap titik porosnya. Secara sistematis, rumus momen inersia dirumuskan sebagai berikut:
I = Ʃm.R2
I = m1.R12+m2.R22+ m3.R32+….+mn.Rn2
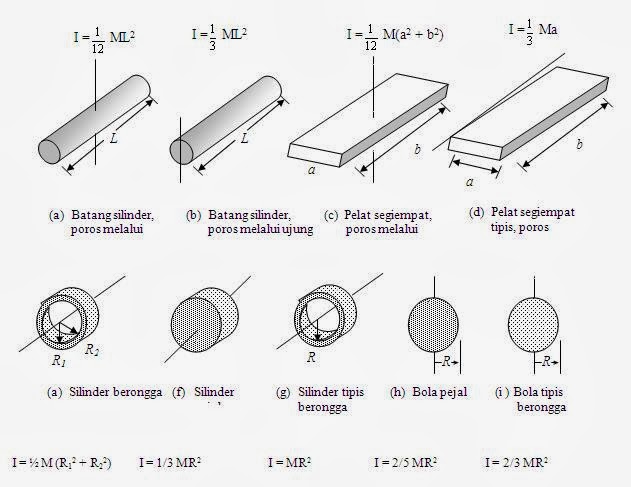
Rumus Momen Inersia Pada Beberapa Benda Khusus
Benda Berupa Titik
Untuk massa benda atau sistem massa berupa titik atau beberapa titik yang terhubung oleh tali atau batang yang massanya diabaikan, maka berlaku:
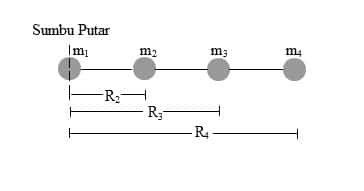
I = Ʃm.R2
Keterangan:
I = Momen Inersia (Kg m2)
m = Massa (Kg)
R = Jarak kr titik poros (m)
Batang Homogen
Batang Homogen adalah batang yang memiliki massa tersebar merata hingga pusat massanya berada di tengah. Untuk batang homogen, maka akan terlihat jelas bahwa terdapat pengaruh letak sumbu putar terhadap momen inersia.
a. Poros berada di Pusat
Jika sumbu putar berada di titik pusat massa maka berlaku:
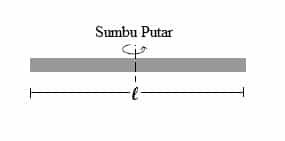
I = 1/12 m.l2
Keterangan :
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg)
Baca Juga : Pesawat Sederhana
b. Poros berada di salah satu ujung
Jika sumbu putar berada pada salah satu ujung batang, maka berlaku:

I = 1/3m.l2
Keterangan:
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg)
c. Poros Bergeser
Jika sumbu putar atau poros berasa disembarang tempat atau tidak berada di ujung maupun pusat, maka berlaku:
Poros Bergeser
I = 1/12 m.l2 + m.(k.l)2
Keterangan:
I = momen inersia (kg m2)
l = panjang batang (m)
k.l = panjang pergeseran (m)
m = massa (kg)
Panjang pergeseran yang dimaksud yaitu seberapa jauh sumbu putar digeser misalkan dari pusat digeser sejauh 1/2l.
Benda Berbentuk Silinder
Silinder Pejal
Benda yang berbentuk silinder pejal seperti katrol atau roda tertentu, maka berlaku rumus:
I = 1/2 m.R2
Keterangan:
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg)
Baca Juga : Tuas atau Pengungkit
Silinder Tipis Berongga
Benda silinder tipis berongga seperti cincin tipis, maka berlaku rumus:
I = m.R2
Keterangan:
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg)
Silinder Berongga Tidak Tipis
Silinder berongga tidak tipis yaitu silinder yang mempunyai jari-jari dalam dan jari-jari luar. Maka berlaku rumus:
I = 1/2 m (R12 + R22)
I = momen inersia (kg m2)
R1 = jari-jari dalam silinder (m)
R2 = jari-jari luar silinder (m)
m = massa (kg)
Benda Berbentuk Bola
Bola Pejal
Apabila benda berbentuk bola pejal, maka berlaku rumus:
I = 2/5m.R2
Keterangan:
I = momen inersia (kg m2)
R = jari-jari bola(m)
m = massa (kg)
Bola Berongga
Rumus yang berlaku untuk bola berongga yaitu:
I = 2/3m.R2
Keterangan:
I = momen inersia (kg m2)
R = jari-jari bola(m)
m = massa (kg)
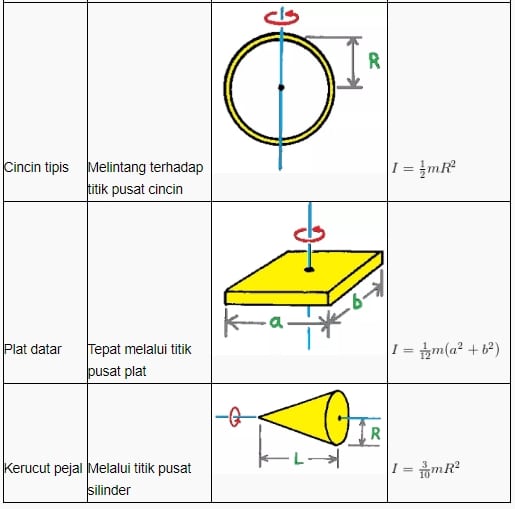
Lebih lengkapnya, perhatikan tabel rumus momen inersia berikut ini:
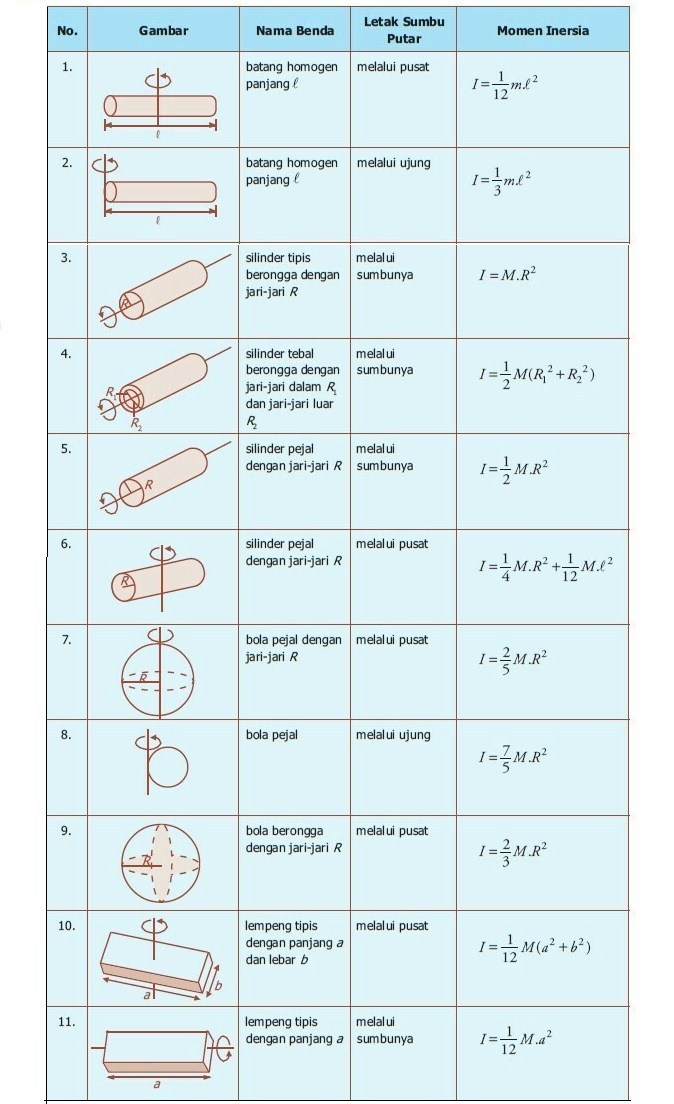
Baca Juga : Hukum Kekekalan Energi
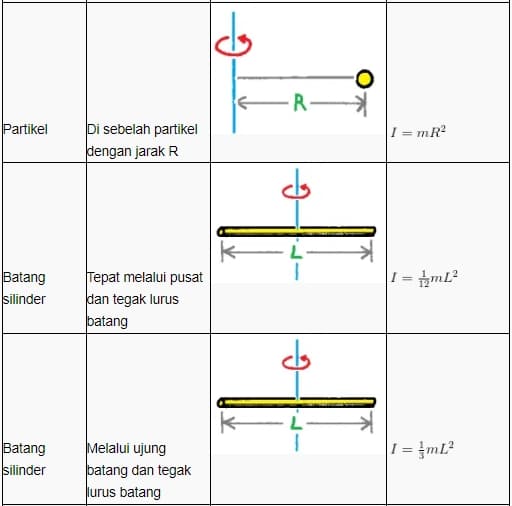
Contoh Penerapan Momen Inersia Dalam Kehidupan Sehari-hari
Apa yang terjadi jika mobil yang melaju dengan kecepatan tinggi direm secara mendadak atau tiba-tiba? Sebenarnya saat itu, terdapat kecendrungan mobil untuk mempertahankan geraknya.
Apakah kecendrungan juga berlaku pada benda diam? Coba letakkan penghapus diatas kertas di atas meja lalu kertas tersebut kamu tarik dengan cepat. Ternyata penghapus tetap berada diatas meja. Maka disimpulkan benda tersebut memiliki sifat alami yang cenderung mempertahankan keadaannya yang diam.
Baca Juga : Dinamika Gerak Rotasi
Contoh Soal Momen Inersia dan Pembahasannya
1. Perhatikan gambar dibawah ini!
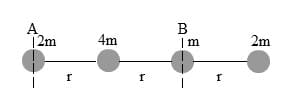
Terdapat empat buah partikel yang dihubungkan oleh sebuah batang yang massanya diabaikan. Tentukan momen inersia sistem partike jika :
a. Diputar terhadap poros A
b. Diputar terhadap poros B
Pembahasan:
a. Diputar terhadap poros A
I = Ʃm.R2
I = 2m(0)2 + 4m (r)2 + m (2r)2 + 2m (3r)2
I = 0 + 4m r2 + 18m r2
I = 26m r2
b. Diputar terhadap poros B
I = Ʃm.R2
I = 2m (2r)2 +4m (r)2 + m (0)2 + 2m (r)2
I = 8m r2 + 4m r2 + 0 + 2m r2
I = 14 m r2
2. Diketahui sebuah batang homogen bermassa 0,6 kg dan panjang 60 cm. Apabila gumpalan lumpur bermassa 20 gram dilempar dan menempel pada salah satu ujung batang, maka tentukan momen inersia sistem melalui pusat batang.
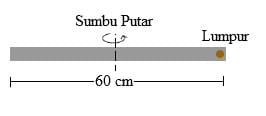
Pembahasan:
I = 1/12m.l2 + mR2
I = 1/12(0,6).(0,6)2 + 0,02(0,3)2
I = 0,018 + 0,0018
I = 0,0198
I = 1,98 x 10-2 kg m2
3. Apabila sebuah silinder pejal bermassa 2 kg dan berjari-jari 0,1 m diputar melalui sumbu silinder dan segumpal lumpur bermassa 0,2 kg menempel pada jarak 0,05 meter dari pinggir silinder, maka hitunglah momen inersia sistem.
Baca Juga : Momentum dan Impuls
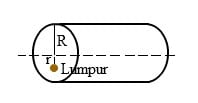
Pembahasan:
I = I silinder + I lumpur
I = 1/2 mR2 + m.r2
I = 1/2 (2).(0,1)2 + 0,2. (0,05)2
I = 0,01 + 0,0005
I = 0,0105
I = 1,05 x 10-2 kg m2
4. Bola bermassa 100 gram dihubungkan dengan seutas tali yang panjangnya 20 cm seperti pada gambar. Momen Inersia bola terhadap sumbu AB adalah…
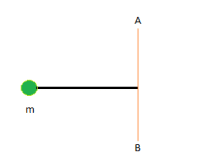
Pembahasan:
Momen inersia sebuah bola bermassa m = 0,1 kg dengan panjang tali r= 0,2 m adalah:
I = mr2
I = (0,1) (0,2)2
I = 4 x 103 kg m2
5. Sebuah sistem dibawah ini terdiri dari 3 partikel. Jika m1= 2 kg, m2= 1 kg dan m3= 2 kg, tentukan momen inersia sistem tersebut jika diputar menurut:
a) poros P
b) poros Q
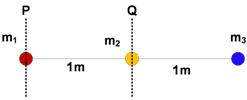
Pembahasan:
Ip = m1r12 + m2r22+ m3r32
Ip = 2.02 + 1.12 + 2.22
Ip = 9 kg m2
IQ = m1r12 + m2r22+ m3r32
IQ = 2.12 + 1.02 + 2.12
IQ = 4 kg m2
Baca Juga : Impuls dalam Fisika
6. Batang pejal bermassa 2 kg dan panjang batang pejal adalah 2 meter. Tentukan momen inersia batang jika sumbu rotasi terletak di tengah batang!
Pembahasan:
Momen inersia batang pejal, sumbu rotasi terletak pada tengah batang
I = 1/12 ml
I = (1/12) (2) (2)2
I = 0,67 kg m2
7. Tentukan momen inersia cakram pejal (padat) bermassa 10 kg dan berjari-jari 0,1 meter, jika sumbu rotasi berada di pusat cakram, sebagaimana ditunjukkan gambar!
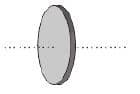
Pembahasan:
Cakram pejal memiliki momen inersia
I = 1/2 mr2
I = (1/2) (10) (0,1)2
I = 0,05 kg m2
8. Tentukan nilai mmomen inersia bola pejal bermassa 15 kg dan berjari-jari 0,1 meter, jika sumbu rotasi berada di pusat bola, sebagaimana ditunjukkan gambar!
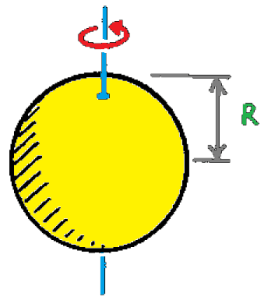
Pembahasan:
Moment inersia bola pejal sumbu rotasi berada di pusat
I = 2/5 mr2
I = (2/5) (15) (0,1)2
I = 0,06 kg m2
9. Perhatikan sebuah batang tipis dengan panjang 4 meter dan bermassa 0,2 kg seperti gambar berikut:
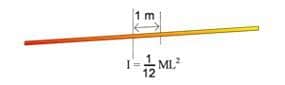
Jika momen inersia dengan poros di pusat massa batang adalah I= 1/12 ML2 tentukan besar momen inersia batang jika poros digeser ke kanan sejauh 1 meter!
Pembahasan:
Momen inersia batang pejal, sumbu putar digeser sebesar r=1 m dari pusat
I = Ip + Mr2
I = 1/12 ML2 +Mr2
I = 1/12 (0,2) (4)2 + (0,2) (1)2
I = 0,46 kg m2
Baca Juga : Tumbukan Fisika
10. Perhatikan gambar dibawah ini!
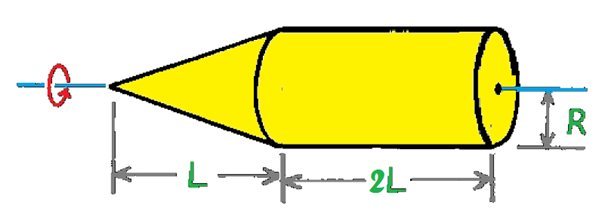
Sebuah benda pejal yang berbentuk seperti kerucut yang menempel pada salah satu ujung silinder diputar dengan sumbu rotasi pada titik pusat silinder seperti yang dapat dilihat pada gambar diatas. Diketahui massa silinder sama dengan massa kerucut yakni sebesar 2 kg, panjang silinder 0,8 meter, dan jari-jari silinder 0,1 meter. Tentukan momen inersia benda tersebut.
Pembahasan:
Untuk menyederhanakan perhitungannya, maka momen inersia tiap geometri benda dihitung terpisah.
I = Isilinder + Ikerucut
I = 2/3 ms Rs2 + 3/10 mk Rk2
Diketahui:
ms = 2 kg dan Rs = 0,1 m;
mk = 2 kg dan Rk = 0,1 m;
Sehingga didapat besar momen inersia benda:
I = 1/2 (2) (0,1)2 + 3/10 (2) (0,12)
I = 0,01 + 3/5 (0,01)
I = 0,01 + 0,006
I = 0,016 kg m2
Demikian pembahasan tentang pengertian momen inersia, rumus dan contoh soal momen inersia benda secara lengkap. Semoga bermanfaat dan jangan lupa ikuti postingan lainnya
Originally posted 2023-10-23 06:54:43.